Aprendemos las fracciones: equivalentes, relación con la unidad…

¡Hola! Estos días estoy repasando las fracciones con mi hija, que está ahora en quinto de primaria. Así que he preparado este post, y os dejo el juego que le he preparado a ella para repasar de una manera más divertida.

¿Qué son las fracciones?

Las fracciones son una parte fundamental de las matemáticas y se utilizan para representar números que no son enteros. Una fracción está compuesta por dos partes: el numerador y el denominador. El numerador indica cuántas partes se toman, mientras que el denominador representa en cuántas partes se divide el todo.

Por ejemplo, en la fracción 3/4, el numerador es 3 y el denominador es 4. Esto significa que estamos tomando tres partes de un total dividido en cuatro partes iguales. Las fracciones pueden ser propias, cuando el numerador es menor que el denominador, o impropias, cuando el numerador es mayor o igual al denominador.

Además, existen las fracciones mixtas, que combinan un número entero con una fracción propia. Es importante entender las fracciones para poder realizar operaciones matemáticas con ellas, como sumar, restar, multiplicar y dividir.

Fracciones equivalentes: ¿qué significa?

Las fracciones equivalentes son aquellas que representan la misma cantidad, pero están escritas de manera diferente. En otras palabras, tienen distintos numeradores y denominadores, pero su valor es el mismo. Por ejemplo, 1/2 y 2/4 son fracciones equivalentes porque ambas representan la mitad de una unidad.

Para determinar si dos fracciones son equivalentes, se puede simplificar o reducir la fracción a su forma más simple, dividiendo el numerador y el denominador por su máximo común divisor. También se pueden encontrar fracciones equivalentes multiplicando o dividiendo tanto el numerador como el denominador por el mismo número.

Conocer las fracciones equivalentes es útil para realizar operaciones matemáticas más sencillas, ya que se pueden utilizar fracciones con números más pequeños. Además, comprender este concepto permite comparar y ordenar fracciones de manera más precisa. En resumen, las fracciones equivalentes son aquellas que representan la misma cantidad, aunque estén escritas de manera diferente.

Comparando fracciones: mayores y menores que la unidad

Comparar fracciones es una habilidad fundamental en las matemáticas y permite determinar si una fracción es mayor o menor que la unidad. Para realizar esta comparación, es necesario tener en cuenta el numerador y el denominador de las fracciones.

• Si el numerador de una fracción es mayor que su denominador, entonces la fracción es mayor que la unidad. Por ejemplo, si tenemos la fracción 3/4, podemos observar que el numerador (3) es mayor que el denominador (4), por lo tanto, esta fracción es mayor que la unidad.
• Por otro lado, si el numerador es menor que el denominador, entonces la fracción es menor que la unidad. Por ejemplo, si tenemos la fracción 1/5, podemos ver que el numerador (1) es menor que el denominador (5), por lo tanto, esta fracción es menor que la unidad.

Comprender cómo comparar fracciones nos ayuda a ordenarlas correctamente y resolver problemas matemáticos de manera más eficiente.

Cómo calcular la fracción de un número

Primero, se toma el número del cual se quiere calcular la fracción y se multiplica por el numerador de la fracción. Luego, se divide el resultado obtenido entre el denominador de la fracción. El resultado final es la fracción del número original.

Por ejemplo, si queremos calcular 3/4 de 20, multiplicamos 20 por 3 (numerador)y luego dividimos el resultado entre 4 (denominador). Esto nos dará como resultado 15, que es 3/4 de 20.

Calcular la fracción de un número es útil en situaciones cotidianas, como determinar cuánto dinero representa un descuento o cuánta comida queda en un recipiente después de servir una porción. Es una habilidad fundamental que los estudiantes deben dominar en quinto grado para comprender mejor el concepto de fracciones y su aplicación en la vida diaria.

Ejemplos prácticos para entender las fracciones

Imagina que tienes una pizza dividida en ocho pedazos iguales. Si te comes tres de esos pedazos, puedes representar esta situación como la fracción 3/8, donde el numerador (3) indica la cantidad de pedazos que te comiste y el denominador (8) representa el total de pedazos en la pizza.

Otro ejemplo es si tienes una barra de chocolate dividida en cuatro partes iguales y te comes dos de esas partes, esto se puede expresar como la fracción 2/4. Sin embargo, esta fracción se puede simplificar dividiendo tanto el numerador como el denominador por 2, lo que resulta en la fracción equivalente 1/2. Estos ejemplos te ayudarán a comprender cómo funcionan las fracciones en situaciones cotidianas y cómo se pueden simplificar para obtener resultados más simples.

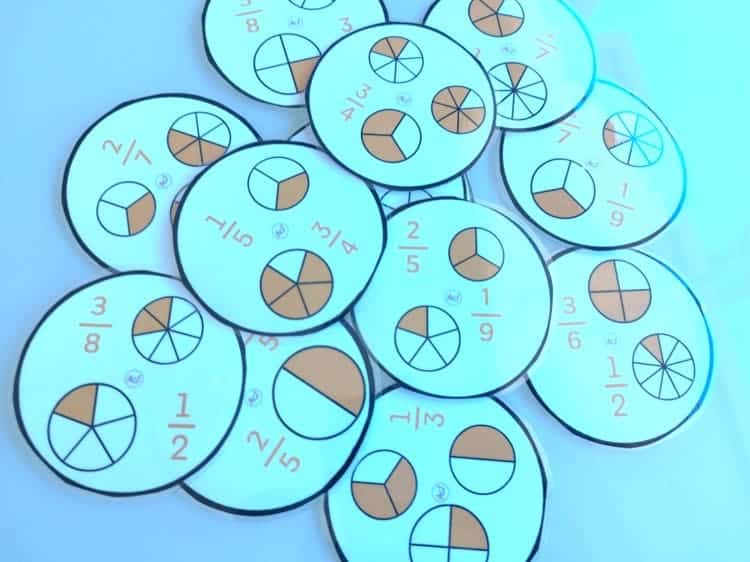
Y ahora os dejo un juego para repasar un poco:

No olvidéis que en el blog también tenéis un juego muy divertido para repasar las fracciones, que podéis descargar en el enlace.